Vetores concorrentes: características, exemplos e exercícios - Ciência - 2023

Contente

• Caracteristicas
• Tipos de vetores
• Notação vetorial
• cartesiano
• Polar
• Analítico
• Esférico
• Operações de vetor simultâneas
• Soma (A + B)
• Diferença (A - B)
• Produto escalar (A. B)
• Produto vetorial (A x B)
• Exemplos: exercícios resolvidos
• Exercício 1
• Exercício 2
• Exercícios propostos
• Referências

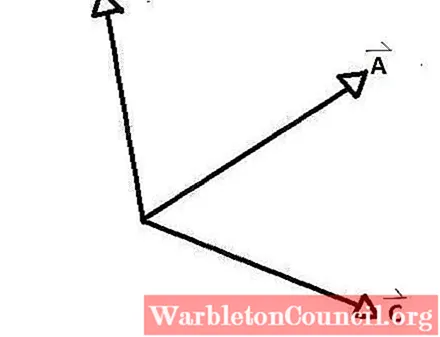
o vetores concorrentes são os grupos de vetores cujos eixos coincidem em um ponto, formando entre cada par um ângulo interno e um ângulo externo. Um exemplo claro é visto na figura abaixo, onde A, B e C são vetores concorrentes entre si.

D e E, ao contrário do resto, não são. Existem ângulos formados entre os vetores concorrentes AB, AC e CB. Eles são chamados de ângulos de relacionamento entre os vetores.

Caracteristicas

-Têm um ponto em comum que coincide com a sua origem: todas as magnitudes dos vetores concorrentes partem de um ponto comum até seus respectivos extremos.

-A origem é considerada como o ponto de ação do vetor: deve ser estabelecido um ponto de ação que será diretamente afetado por cada um dos vetores concorrentes.

-Seu domínio no plano e espaço é R² e R³ respectivamente: os vetores concorrentes são livres para cobrir todo o espaço geométrico.

-Permite diferentes notações no mesmo grupo de vetores. De acordo com os ramos de estudo, diferentes notações estão presentes nas operações com vetores.

Tipos de vetores

O ramo de vetores possui múltiplas subdivisões, algumas das quais podem ser nomeadas: paralela, perpendicular, coplanar, correspondente, oposta e unitária. Os vetores concorrentes são listados aqui e, como todos os mencionados acima, eles têm muitas aplicações em diferentes ciências.

São muito comuns no estudo de vetores, pois representam uma generalização útil nas operações com eles. Tanto no plano quanto no espaço, vetores concorrentes são comumente usados ​​para representar diferentes elementos e estudar sua influência em um sistema particular.

Notação vetorial

Existem várias maneiras de representar um elemento vetorial. Os principais e mais conhecidos são:

cartesiano

Proposto por esta mesma abordagem matemática, denota os vetores com um triplo correspondente às magnitudes de cada eixo (x, y, z)

A: (1, 1, -1) Espaço A: (1, 1) Plano

Polar

Eles servem apenas para denotar vetores no plano, embora no cálculo integral seja atribuído o componente de profundidade. É composto com uma magnitude linear r e um ângulo em relação ao eixo polar Ɵ.

A: (3, 45⁰ ) Plano A: (2, 45⁰ , 3) Espaço

Analítico

Eles definem as magnitudes do vetor usando os versores. Os versores (i + j + k) representam os vetores unitários correspondentes aos eixos X, Y Y

A: 3i + 2j - 3k

Esférico

Eles são semelhantes à notação polar, mas com a adição de um segundo ângulo que varre o plano xy simbolizado por δ.

A: (4, 60^ou , π/4 )

Operações de vetor simultâneas

Os vetores concorrentes são usados ​​principalmente para definir operações entre vetores, porque é mais fácil comparar os elementos dos vetores quando eles são apresentados simultaneamente.

Soma (A + B)

A soma dos vetores concorrentes visa encontrar o vetor resultante V_r. Que, segundo o ramo de estudo, corresponde a uma ação final

Por exemplo: 3 cordas {A, B, C} são amarradas a uma caixa, cada ponta da corda é segurada por um sujeito. Cada um dos 3 sujeitos deve puxar a corda em uma direção diferente do outro 2.

A: (ax, ay, az) B: (bx, by, bz) C: (cx, cy, cz)

A + B + C = (ax + bx + cx; ay + by + cy; az + bz + cz) = V_r

A caixa só pode se mover em uma direção, portanto V_r ele indicará a direção e a sensação de movimento da caixa.

Diferença (A - B)

Existem muitos critérios em relação à diferença entre vetores, muitos autores optam por excluí-la e afirmam que apenas a soma entre os vetores é estipulada, onde a diferença é sobre a soma do vetor oposto. A verdade é que os vetores podem ser subtraídos algebricamente.

A: (ax, ay, az) B: (bx, by, bz)

A - B = A + (-B) = (ax-bx; ay-by; az-bz) = [ax + (-bx); ay + (-by); az + (-bz)]

Produto escalar (A. B)

Também conhecido como produto escalar, ele gera um valor escalar que pode ser relacionado a várias magnitudes, dependendo do ramo de estudo.

Para geometria, indique a área do paralelogramo formada pelo par de vetores concorrentes através do método do paralelogramo. Para a física mecânica, defina o trabalho realizado por uma força F ao mover um corpo à distância Δr.

ѡ = F . Δr

Como seu nome indica, ele gera um valor escalar e é definido da seguinte forma:

Sejam os vetores A e B

A: (ax, ay, az) B: (bx, by, bz)

-Forma analítica:

(A. B) = | A |. | B | .Cos θ

Onde θ é o ângulo interno entre os dois vetores

-Forma algébrica:

(A.B) = (ax.bx + ay.by + az.bz)

Produto vetorial (A x B)

O produto vetorial ou produto pontual entre dois vetores, define um terceiro vetor C que tem a qualidade de ser perpendicular a B Y C. Na física, defina o vetor de torque τ elemento básico da dinâmica rotacional.

-Forma analítica:

| A x B | = | A |. | B | .Sen θ

-Forma algébrica:

(A x B) = = (ax. por - ay. bx) - (ax. bz - az. bx) j + (ax. por - ay. bx) k

-Movimento relativo: r_{A / B}

A base da relatividade é o movimento relativo e os vetores concorrentes são a base do movimento relativo. Posições, velocidades e acelerações relativas podem ser deduzidas aplicando a seguinte ordem de idéias.

r _{A / B} = r_PARA - r_B ; Posição relativa de A em relação a B

v _{A / B} = v_PARA - v_B ; Velocidade relativa de A em relação a B

para _{A / B} = a_PARA - para_B ; Aceleração relativa de A em relação a B

Exemplos: exercícios resolvidos

Exercício 1

Sejam A, B e C vetores concorrentes.

A = (-1, 3, 5) B = (3, 5, -2) C = (-4, -2, 1)

-Defina o vetor resultante V_r = 2A - 3B + C

2A = (2 (-1), 2 (3), 2 (5)) = (-2, 6, 10)

-3B = (-3 (3), -3 (5), -3 (-2)) = (-9, -15, 6)

V_r = 2A + (-3B) + C = (-2, 6, 10) + (-9, -15, 6) + (-4, -2, 1)

V_r =  ( [-2+(-9)+(-4)] ; [6+(-15)+(-2)] ; (10+6+1) )

V_r = ( -15 , -11 , 17 )

-Defina o produto escalar (A. C)

(A. C) = (-1, 3, 5). (-4, -2, 1) = (-1) (-4) + 3 (-2) + 5 (1) = 4 - 6 + 5

(A. C) = 3

-Calcule o ângulo entre A e C

(A. C) = | A |. | C |. Cos θ Onde θ é o menor ângulo entre os vetores

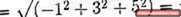
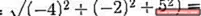
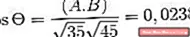
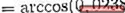
θ = 88,63⁰

 -Encontrar um vetor perpendicular a A e B

Para isso é necessário definir o produto vetorial entre (-1, 3, 5) e (3, 5, -2). Como explicado antes, uma matriz 3 x 3 é construída onde a primeira linha é composta de vetores unitários triplos (i, j, k). Em seguida, a 2ª e 3ª linhas são formadas pelos vetores para operar, respeitando a ordem operacional.

(A x B) =   = [ (-1) . 5 – (3 . 3) ] Eu  – [ (-1) . (-2) – (5 . 3) ] j + [ (-1) . 5 – (3 . 3) ] k

(A x B) =  ( -5 – 9) EU - (2 - 15) j + (-5 - 9) k

(A x B) =  –14 I + 13 j - 14 k

Exercício 2

Deixe V_para e V_b os vetores de velocidade de A e B, respectivamente. Calcule a velocidade de B vista de A.

V_para = (3, -1, 5) V_b = ( 2 , 5 , -3 )

Neste caso, a velocidade relativa de B em relação a A é solicitada V_BA

V_BA = V_B - V_PARA

V_BA = ( 2 , 5 , -3 ) – ( 3 , -1 , 5 ) = ( -1 , 6 , -8 )

Este é o vetor de velocidade de B visto de A. Onde um novo vetor de velocidade de B é descrito tomando a referência de um observador posicionado em A e movendo-se com a velocidade de A.

Exercícios propostos

1-Construa 3 vetores A, B e C que sejam concorrentes e relacione 3 operações entre eles através de um exercício prático.

2-Deixe os vetores A: (-2, 4, -11), B: (1, -6, 9) e C: (-2, -1, 10). Encontre vetores perpendiculares a: A e B, C e B, A soma A + B + C.

4-Determine 3 vetores que sejam perpendiculares entre si, sem levar em consideração os eixos coordenados.

5-Defina o trabalho realizado por uma força que levanta um bloco de massa de 5 kg, do fundo de um poço de 20m de profundidade.

6-Mostre algebricamente que a subtração dos vetores é igual à soma do vetor oposto. Justifique seus postulados.

7-Denote um vetor em todas as notações desenvolvidas neste artigo. (Cartesiano, polar, analítico e esférico).

8-As forças magnéticas exercidas sobre um ímã que repousa sobre uma mesa, são dadas pelos seguintes vetores; V: (5, 3, -2), T: (4, 7, 9), H: (-3, 5, -4). Determine em que direção o ímã se moverá se todas as forças magnéticas agirem ao mesmo tempo.

Referências

1. Geometria Euclidiana e Transformações. Clayton W. Dodge. Courier Corporation, 1º de janeiro 2004
2. Como resolver problemas de matemática aplicada L. Moiseiwitsch. Courier Corporation, 10 de abril 2013
3. Conceitos básicos de geometria. Walter Prenowitz, Meyer Jordan. Rowman & Littlefield, 4 de outubro. 2012
4. Vetores. Rocío Navarro Lacoba, 7 de junho. 2014
5. Álgebra Linear. Bernard Kolman, David R. Hill. Pearson Education, 2006