Transformações lineares: propriedades, para que servem, tipos, exemplos - Ciência - 2023
science
Contente
- Propriedades de transformações lineares
- Propriedade 1
- Propriedade 2
- Propriedade 3
- Propriedade 4
- Elementos de transformação linear
- Para que servem as transformações lineares?
- Tipos de transformações lineares (classificação)
- Transformações lineares subjetivas
- Transformações lineares bijetivas
- Endomorfismos
- Automorfismos
- Transformações lineares especiais
- Operador linear
- Transformação zero
- Transformação de identidade
- Transformação definida por uma matriz
- Função linear
- Formulários
- Exemplos de transformações lineares
- Exemplo 1
- Exemplo 2
- Exercícios resolvidos
- - Exercício 1
- Solução
- Primeira condição
- Segunda condição
- - Exercício 2
- Solução
- Referências
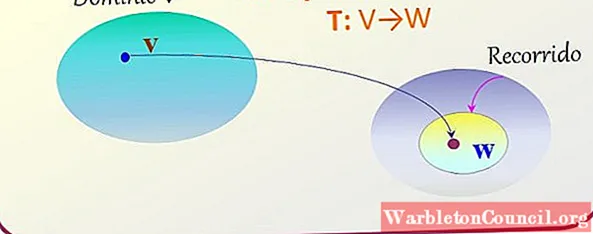
UMA transformação linear, que chamaremos simplesmente de T, relaciona os elementos de dois espaços vetoriais V e W, atribuindo a cada vetor v pertencente a V um único vetor W que pertence a W, por meio de uma operação específica.
Essa transformação atende a duas condições:
- Condição 1
Refere-se à adição, para que uma transformação T seja linear, deve ser verdade que:
T (v + W) = T (v) + T (W)
- Condição 2
A segunda condição representa a homogeneidade na multiplicação de um escalar por um vetor:
T (cv) = c⋅T (v)
A transformação linear, como o próprio nome indica, é responsável por mapear ou transformar elementos de V em elementos de W.
A notação para funções também é usada no caso de transformações lineares, portanto, o domínio de V é o conjunto de elementos (vetores) a serem transformados, enquanto o codomínio ou caminho é o conjunto resultante.
Um exemplo de transformação linear é:
Para indicar que uma transformação será realizada, utilize a letra T. A transformação será aplicada a um vetor v cujos componentes são xey, que foi representado por uma única matriz de coluna. O resultado é outro vetor W cujos componentes são xe 0, também representados por uma matriz de coluna.
Portanto, esta é uma transformação do espaço vetorial R2 em direção ao espaço vetorial R2, que em síntese é escrito assim:
T: R2 → R2
Se tivermos o vetor:
A transformação nos devolve:
E assim com qualquer vetor de R2. No exemplo 1 será verificado que esta transformação é linear.
Propriedades de transformações lineares
Suponha uma transformação linear T de V para W, na qual os vetores v Y ou pertencem a V, então as seguintes propriedades são verdadeiras:
Propriedade 1
T (0) = 0
Onde0 é o vetor nulo.
Propriedade 2
T (-v) = - T (v)
Propriedade 3
T (ou – v) = T (ou) - T (v)
Propriedade 4
Estar v = c1v1 + c2v2 +…. + cnvn
Então:
T (c1v1 + c2v2 +…. + cnvn) = c1 T (v1) + c2 T (v2) +…. + cn T (vn)
Elementos de transformação linear
Sejam V e W os espaços vetoriais mencionados acima, onde a transformação linear T transforma os elementos de V em W. Podemos definir os seguintes elementos:
–Kernel T ou kernel: é um subconjunto do domínio denotado por N (T) ou ker (T) e inclui todos os elementos de V, de modo que:
T (v) = 0.
A transformação linear T (v) = 0 se chama transformação nula.
Naturalmente, o vetor nulo v = 0 ele satisfaz esta condição de qualquer maneira, mas o kernel consiste no conjunto de vetores não nulos que também o satisfazem, para um dado T.
–Imagem de T: é o conjunto de vetores pertencentes a W tais que são a imagem de pelo menos algum vetor em V. É denotado como EU SOU T) y é um subconjunto do espaço vetorial W.
Esses elementos nos ajudarão a classificar as transformações lineares posteriormente.
Para que servem as transformações lineares?
Inicialmente, as transformações lineares funcionam com espaços vetoriais, constituídos por vetores. Freqüentemente associamos vetores a forças e outras grandezas físicas, porém, no processamento digital de imagens, um pixel pode ser representado por um vetor.
Nesse caso, a imagem pode ser manipulada por convenientes transformações lineares para obter os efeitos desejados, por exemplo, projetar, girar, localizar a imagem espelhada ou redimensioná-la sem alterar as dimensões relativas.
As transformações lineares também são amplamente utilizadas na economia e na tomada de decisões, por exemplo, para saber a quantidade de matéria-prima necessária para fabricar um determinado lote de produtos.
A quantidade de peças necessárias para montar os diversos modelos que uma fábrica produz pode ser trabalhada por meio de um arranjo matricial, como veremos adiante.
Tipos de transformações lineares (classificação)
Como funções, as transformações lineares podem ser:
-Injetivos ou monomorfismos
-Bijetivos ou epimorfismos
-Overjetivos ou isomorfismos
Existem também os seguintes tipos:
-Endomorfismos
-Automorfismos.
Transformações lineares injetivas
Sejam V e W espaços vetoriais e T uma transformação linear T: V → W. T é injetiva quando:
Ker (T) = 0
Transformações lineares subjetivas
Se V e W são espaços vetoriais tais que T: V → W, dizemos que T é bijetivo quando:
Im (T) = W
Transformações lineares bijetivas
Uma transformação linear T: V → W é bijetiva quando é tanto injetiva quanto sobrejetora. Portanto, é verdade que:
Ker (T) = 0 e Im (T) = W
Endomorfismos
São transformações lineares nas quais o domínio e o codomínio coincidem.
Automorfismos
Esta classe de transformações lineares são endomorfismos bijetivos.
Transformações lineares especiais
Operador linear
Uma transformação linear T: V → V, que vai de um espaço vetorial para o mesmo espaço vetorial é chamada operador linear.
Transformação zero
Mencionado acima, a transformação zero é importante para encontrar o núcleo de uma transformação linear:
T: V → W tal que T (v) = 0 para qualquer v.
Transformação de identidade
T: V → V tal que T (v) = v para qualquer v.
Transformação definida por uma matriz
T: V → W tal que T (v) = Av, onde A é uma matriz e v é um vetor de coluna.
Função linear
As funções lineares do tipo y = mx são transformações lineares. Tome por exemplo y = 3x e veja se ele atende às duas condições no início, testando com quaisquer dois valores a e b:
f (a + b) = 3 (a + b) = 3a + 3b = f (a) + f (b)
f (ka) = 3 (ka) = k⋅ (3a) = k⋅f (a)
É efetivamente uma transformação linear.
Formulários
As transformações lineares têm aplicações matemáticas, como:
-Rotação de eixos coordenados.
-Na solução de sistemas de equações diferenciais lineares.
-Problemas de autovalores e autovetores.
E também têm aplicações em outros campos da ciência, por exemplo, mecânica, mecânica quântica e economia, entre outras áreas.
Exemplos de transformações lineares
Exemplo 1
Em muitos problemas de mecânica, precisamos encontrar a projeção de um vetor v pertencente ao espaço, em um determinado plano. Este vetor v pode representar, por exemplo, uma força.
Suponha que você queira projetar o vetor v = Quando o aplicamos ao vetor v obtemos um vetor cujo componente z desaparece. Geometricamente é representado assim, com a projeção de v no plano xy como o vetor vermelho de dois componentes. Suponha que você tenha uma fábrica que produz três tipos de carrinhos de brinquedo: C1, C2 e C3, para os quais você precisa de três tipos de peças em certas quantidades para fazer cada tipo de carrinho: - Eixos ou parte A -Rodas ou parte B -Chassi ou parte C Para cada tipo de carrinho, a quantidade de peças é diferente, pois os modelos são diferentes. Podemos organizar as quantidades de forma ordenada em uma matriz 3 × 3, em que as colunas são encabeçadas pelo tipo de carrinho, e as linhas correspondem ao número de peças necessárias para fazer cada modelo. Este é um exemplo de uma transformação dada por uma matriz que se pareceria com esta: Se a fábrica receber um determinado pedido de compra, que consiste em x quantidade de C1, Y de C2 e z De C3, quantas peças A, B e C você precisa ter disponíveis para montar os carrinhos de pedidos? Devemos encontrar uma transformação linear T (x) tal que: Para obter o vetor Y: Isso nos dará o número de peças que devemos ter disponíveis. No exercício resolvido 2, avaliamos a eficiência das transformações lineares para encontrar o número de peças necessárias para cumprir uma determinada ordem. Verifique se a seguinte transformação T: R2 → R2 é linear: Para isso, é necessário verificar se a transformação atende às duas condições descritas no início, primeiro a adição e depois o produto de um escalar por um vetor. Então você tem que pegar dois vetores v Y ou pertencente a R2, escrevendo-os usando notação de matriz ou especificando os componentes. Esses vetores são: v = x1, Y1 ou = x2, Y2 -Lembrando que os vetores são adicionados componente a componente, deve-se verificar que: T (v+ou) = T (v) + T (ou) T (v+ou) = T (x1+ x2 ; Y1 + e2) A partir daqui, é obtido que: T (x1+ x2 ; Y1 + e2) = (x1+ x2; 0) - Por outro lado, ao aplicar a transformação a cada vetor separadamente: T (x1, Y1) + T (x2, Y2) = (x1, 0) + (x2,0) Ao adicionar os vetores resultantes, obtemos efetivamente: W = (x1+ x2; 0) Como os dois resultados são idênticos, a primeira condição é satisfeita. Agora vamos verificar que ao multiplicar por um escalar c, isso pode ser deixado de fora da transformação: T (cv) = c⋅T (v) Sean: v = x1, Y1 c.v = c⋅x1, c⋅y1 Então: T (cv) = T (c⋅x1, c⋅y1 ) = (c⋅x1 , 0) Mas sabemos da etapa anterior que T (v) = T (x1, Y1 ) = (x1 , 0). Portanto, como as duas expressões são idênticas, a segunda condição também é satisfeita e a transformação é linear. Uma fábrica de carros de brinquedo monta três modelos de veículos: C1, C2 e C3, para os quais necessita das partes A, B e C que são respectivamente eixos, rodas e chassis. As quantidades necessárias estão na seguinte tabela: A fábrica foi solicitada a construir 12 modelos C1, 22 C2 e 16 C3. Quantas peças A, B e C são necessárias para concluir o pedido? É aplicada a transformação linear T (x) = Y, cujo resultado é o produto entre matrizes: Eles são necessários no total: -96 eixos -256 rodas -50 chassis.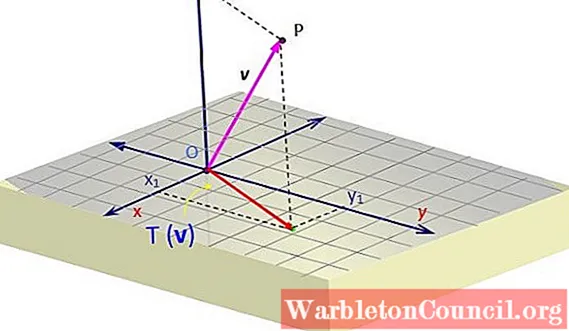
Exemplo 2
Exercícios resolvidos
- Exercício 1
Solução
Primeira condição
Segunda condição
- Exercício 2

Solução

Referências
