Movimento circular uniforme (M.C.U.): fórmulas, características - Ciência - 2023

Contente

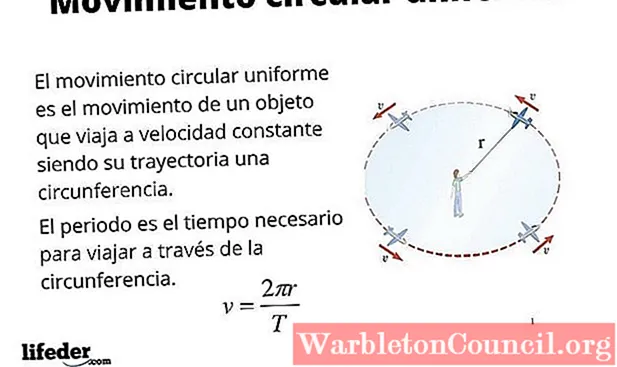
Uma partícula tem movimento circularuniforme (M.C.U.) quando sua trajetória é uma circunferência e também a percorre com velocidade constante. Muitos objetos, como peças de máquinas e motores, por exemplo, possuem esse tipo de movimento, entre os quais estão discos rígidos de computadores, pás de ventiladores, eixos e muitos outros.

O movimento circular uniforme também é uma boa aproximação para o movimento de alguns corpos celestes como a Terra. Na verdade, a órbita da Terra é elíptica, conforme indicado pelas leis de Kepler. No entanto, a excentricidade da órbita é pequena e como uma primeira aproximação pode ser considerada circular, o que simplifica alguns cálculos, como encontrar a velocidade da Terra quando ela se move ao redor do sol.

Na descrição do movimento circular uniforme, os mesmos parâmetros são usados como no movimento retilíneo, a saber: posição, deslocamento, tempo, velocidade e aceleração.

Aceleração? Sim, de fato, o movimento circular uniforme é acelerado, mesmo quando sua velocidade v seja constante. Isso ocorre porque a velocidade v, que é um vetor e, portanto, está em negrito, muda continuamente sua direção conforme o objeto ou partícula gira. Qualquer mudança em v é produzida por uma aceleração que, como se verá, é dirigida para o centro do caminho circular.

O movimento circular uniforme é o movimento no plano xy, portanto, é um movimento em duas dimensões. No entanto, é possível expressar de forma mais conveniente pelo ângulo θ que a partícula varre, medido em relação ao eixo horizontal ou outro eixo de referência adequado.

Mesmo que seja um objeto estendido, suas partículas sempre varrem o mesmo ângulo, mesmo que tenham coordenadas diferentes (x, y).

Características do movimento circular uniforme

As características do movimento circular uniforme podem ser resumidas da seguinte forma:

-A trajetória é uma circunferência, portanto é um movimento no plano.

-A rapidez v é constante, mas a velocidade v não, porque ele muda continuamente de direção e direção para acomodar a virada do celular.

-O vetor velocidade v é sempre tangencial à circunferência e perpendicular à direção radial.

-A velocidade angular ω é constante.

-Apesar de ser uniforme, há uma aceleração para explicar essas mudanças no sentido da velocidade. Essa aceleração é a aceleração centrípeta.

-A aceleração centrípeta e a velocidade são perpendiculares uma à outra.

-É um movimento periódico ou repetitivo, portanto, para ele estão definidas as magnitudes de período e frequência.

Fórmulas de movimento circular uniforme

Neste esquema, há uma partícula P girando no sentido anti-horário com MCU, de acordo com a direção e sentido do vetor velocidade v desenhado.

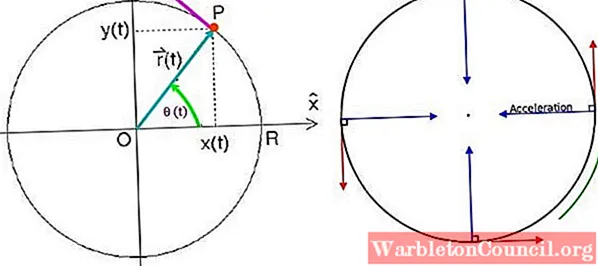
Para especificar o vetor posição é necessário ter um ponto de referência e o ponto ideal é o centro da circunferência O que coincide com o centro do sistema de coordenadas cartesianas no plano xy.

Vetor de posição

É denotado como r (t) e é direcionado da origem ao ponto P onde a partícula está localizada. Em um dado instante t, em coordenadas cartesianas, é escrito como:

r (t) = x (t) Eu + y (t) j

Onde Eu Y j são os vetores unitários perpendiculares às direções x e Y respectivamente. No gráfico, pode-se ver que o módulo vetorial r (t) sempre vale a pena R, o raio da circunferência. Se θ é o ângulo formado r com o eixo horizontal, a posição também é igual a:

r (t) = [Rcos θ(t)] Eu + [Rsen θ(t)] j

O ângulo que forma r (t) com o eixo horizontal é um ângulo central e seu valor é:

θ = s / R

Onde s é o arco de circunferência percorrido e R o raio. Dito ângulo θ é uma função do tempo, então pode ser escrito θ = θ (t), ligar posição angular.

Como a velocidade é constante, a partícula descreve ângulos iguais em tempos iguais e em analogia com o movimento retilíneo uniforme, está escrito:

θ = θ (t) = θ_ou + ωt

Aquiθ_ou é o ângulo inicial medido em radianos em relação ao eixo de referência, pode ser 0 ou qualquer valor e ω é a velocidade angular.

Velocidade angular e velocidade linear

A velocidade angular é a primeira derivada da posição angular e é indicada como ω. Seu valor é constante para movimento circular uniforme, uma vez que ângulos iguais são varridos em tempos iguais. Em outras palavras:

As unidades de velocidade linear em movimento circular uniforme são as mesmas do movimento linear: m / s (no Sistema Internacional SI), km / h, cm / s e outros.

Aceleração centrípeta

Na figura abaixo, há uma partícula que se move no sentido horário ao redor da circunferência com velocidade constante. Isso significa que o vetor velocidade sempre tem o mesmo módulo, mas muda de direção para acomodar a circunferência.

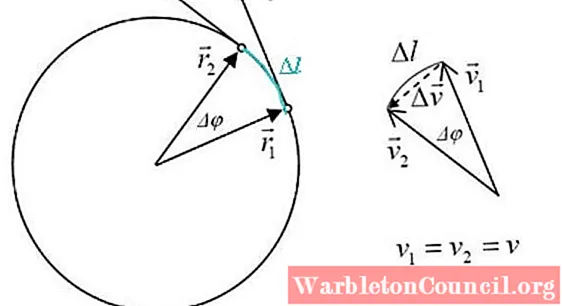
Qualquer mudança na velocidade resulta em aceleração, que por definição é:

O triângulo formado por v₂, v₁ e Δv é semelhante ao triângulo de lados r₂, r₁ e Δeu, onde Δφ é o ângulo central. As magnitudes de r₂ Y r₁eles são iguais, então:

r₂ = r₁= r

Então, de ambos os triângulos, temos essas relações para o ângulo:

Δφ = Δr / r; Δφ = Δv / v

O negrito não é necessário, pois a medida do ângulo depende das magnitudes desses vetores. Combinando as expressões anteriores, segue-se que:

Período e frequência

Como o movimento circular é repetitivo, o período é definido T o mesmo que o tempo que o celular leva para fazer uma volta completa. Como o comprimento da circunferência do raio R é 2πR, o ângulo varrido em radianos na volta completa é 2π radianos e leva tempo T, a velocidade angular é:

ω = 2π / T

T = 2π / ω

O período de movimento circular uniforme é medido em segundos no Sistema Internacional.

Por sua vez, a frequência F é o número de voltas por unidade de tempo e é o recíproco ou inverso do período:

f = n / t = 1 / T

A unidade de frequência no Sistema Internacional é s^-1.

Exemplos de movimento circular uniforme

Muitos objetos giram para produzir vários efeitos: rodas, discos e turbinas. Uma vez que a velocidade de operação é alcançada, a rotação é normalmente executada a uma velocidade constante. O movimento circular é tão comum na vida cotidiana que você quase nunca pensa sobre isso, então aqui estão alguns exemplos que ilustram muito bem:

O movimento da Terra

A Terra e os demais planetas do Sistema Solar se movem em trajetórias elípticas de pequena excentricidade, exceto Mercúrio, o que significa que à primeira aproximação, pode-se supor que seu movimento é circular uniforme.

Com isso você tem uma boa ideia da velocidade de translação em torno do Sol, já que no caso da Terra o período do movimento é conhecido: um ano ou 365 dias.

Partículas na borda de um disco

As partículas que giram na ponta de uma velha vitrola ou na lâmina de um ventilador seguem um movimento circular uniforme, assim que o aparelho atinge sua velocidade de reprodução.

Telescópio espacial Hubble

O Telescópio Espacial Hubble circunda a Terra a cerca de 7550 m / s.

Centrífugas

As máquinas de lavar realizam um processo de centrifugação para espremer as roupas, que consiste em girar o tambor do recipiente em alta velocidade. Os secadores também giram por um período de tempo em um movimento circular uniforme.

A centrifugação também é usada em laboratórios para separar compostos, por exemplo, e assim separar seus constituintes por diferença de densidades. Sempre que falamos em centrifugação, há um movimento circular uniforme, pelo menos por um tempo.

Regadores de jardim

Muitos aspersores de jardim giram a uma velocidade constante para que o solo seja regado uniformemente.

Esportes

No lançamento do martelo, por exemplo, que é uma disciplina olímpica, o atleta gira uma bola de metal com força por meio de um cabo de aço preso à empunhadura. O objetivo é mandar a bola o mais longe possível, mas sem sair de uma determinada área.

Exercício resolvido

Uma partícula se move em um círculo de raio 2m com uma velocidade constante v = 8 m / s, no sentido anti-horário. Inicialmente, a partícula estava em r = +2 j m. Calcular:

a) A velocidade angular ω

b) Sua posição angular θ (t)

c) O período de movimento

d) Aceleração centrípeta.

e) Posição da partícula após t = π / 4 s

Solução para

Da fórmula v = Rω segue-se que:

ω = v / R = (8 m / s) / 2m = 4rad ∙ s^-1

Solução b

Tomando o eixo x positivo como eixo de referência, a partícula está inicialmente em 90º = π / 2 radianos em relação ao referido eixo, pois a afirmação diz que a posição inicial é +2 j m, ou seja, a partícula está em y = 2m quando o movimento começa a seguir.

θ = θ (t) = θ_ou + ωt = π / 2 + 4t

Solução c

T = 2π / ω = 2π / 4 s = 0,5 π s

Solução d

a = v² / R = (8 m / s)² / 2 m = 32 m / s²

Solução e

θ (t) = π / 2 + 4t → θ (π / 4) = π / 2 + 4 ∙ (π / 4) = 3π / 2 radianos

Isso significa que após esse tempo, a partícula está na posição y = -2m j. Faz sentido porque t = π / 4 s é a metade do período, portanto a partícula viajou em um ângulo de 180º no sentido anti-horário de sua posição inicial e tem que estar apenas na posição oposta.

Referências

Figueroa, D. (2005). Série: Física para Ciência e Engenharia. Volume 1. Cinemática. Editado por Douglas Figueroa (USB).
Giambattista, A. 2010. Física. 2ª Ed. McGraw Hill.
Sears, Zemansky. 2016. Física Universitária com Física Moderna. 14º. Ed. Volume 1. Pearson.
Serway, R., Jewett, J. (2008). Física para Ciência e Engenharia. Volume 1. 7º. Ed. Cengage Learning.
Zapata, F. Movimento Circular. Recuperado de: francesphysics.blogspot.com.