Equações de primeiro grau: fórmula, como resolvê-los, exemplo, exercícios - Ciência - 2023

Contente

As primeiro grau ou equações lineares com um desconhecido são aqueles que podem ser expressos como a soma de dois termos, da seguinte forma:

ax + b = 0

Onde a e b, com para ≠ 0, são números reais R ou também complexos C. Para resolvê-lo, os termos são transpostos, o que significa mudar os termos de um lado para o outro da igualdade.

Para resolver a incógnita, transpõe-se o termo + b, que deve ir para o lado direito da igualdade com o sinal alterado.

ax = -b

Então, o valor de x é limpo, desta forma:

x = - b / a

Como exemplo, vamos resolver a seguinte equação:

6x - 5 = 4

Transpomos o termo -5 para o lado direito com um sinal alterado:

6x = 4 + 5

Isso é equivalente a adicionar 5 a ambos os lados da equação original:

6x - 5 + 5 = 4 + 5 → 6x = 9

E agora resolvemos o desconhecido "x":

x = 9/6 = 3/2

O que é equivalente a dividir os dois lados da igualdade por 6. Portanto, podemos usar o seguinte para obter a solução:

-Você pode adicionar ou subtrair a mesma quantidade para ambos os lados da igualdade em uma equação, sem alterá-la.

-Você também pode multiplicar (ou dividir) pelo mesmo valor todos os termos à esquerda e à direita da equação.

-E se ambos os membros de uma equação forem elevados à mesma potência, a igualdade também não é alterada.

Como resolver equações de primeiro grau

A solução de uma equação de primeiro grau também é conhecida como sua raiz. É o valor de x que converte a expressão original em uma igualdade. Por exemplo em:

5x = 8x - 15

Se substituirmos x = 5 nesta equação, obteremos:

5⋅5 = 8⋅5 – 15

25 = 40 – 15

25 = 25

Já que as equações lineares de primeiro grau vêm em muitas formas, que às vezes não são óbvias, há uma série de regras gerais que incluem várias manipulações algébricas, a fim de encontrar o valor do desconhecido:

-Primeiro, se houver operações indicadas, elas devem ser realizadas.

-Os símbolos de agrupamento como parênteses, colchetes e colchetes, se existirem, devem ser excluídos mantendo-se os sinais apropriados.

-Os termos são transpostos para colocar todos aqueles que contêm o desconhecido de um lado da igualdade e aqueles que não o contêm do outro.

-Então, todos os termos semelhantes são reduzidos para chegar ao formulário ax = -b.

–E a última etapa é esclarecer o desconhecido.

Interpretação gráfica

A equação de primeiro grau elevada no início pode ser derivada da equação da reta y = mx + c, fazendo y = 0. O valor resultante de x corresponde à interseção da reta com o eixo horizontal.

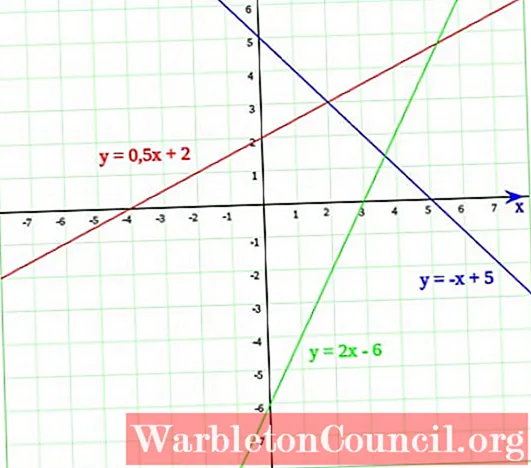
Na figura a seguir, existem três linhas. Começando com a linha verde, cuja equação é:

y = 2x - 6

Fazendo y = 0 na equação da linha, a equação de primeiro grau é obtida:

2x - 6 = 0

Cuja solução é x = 6/2 = 3. Agora, quando detalhamos o gráfico, é fácil ver que, de fato, a linha cruza o eixo horizontal em x = 3.

A linha azul intercepta o eixo x em x = 5, que é a solução para a equação –x + 5 = 0. Finalmente, a linha cuja equação é y = 0,5x + 2 intercepta o eixo x em x = - 4, que é facilmente visto a partir da equação de primeiro grau:

0,5 x + 2 = 0

x = 2 / 0,5 = 4

Exemplos de equações lineares simples

Equações inteiras

São aqueles em cujos termos não há denominadores, por exemplo:

21 - 6x = 27 - 8x

Sua solução é:

-6x + 8x = 27 - 21

2x = 6

x = 3

Equações fracionárias

Essas equações contêm pelo menos um denominador diferente de 1. Para resolvê-las, é aconselhável multiplicar todos os termos pelo mínimo múltiplo comum (MMC) dos denominadores, a fim de eliminá-los.

A seguinte equação é do tipo fracionário:

Como esses números são pequenos, não é difícil ver que m.c.m (6, 8,12) = 24. Esse resultado é facilmente obtido expressando os números como um produto de números primos ou seus poderes, vejamos:

6 = 3.2

8 = 2³

12 = 2²⋅3

O mínimo múltiplo comum é determinado multiplicando os fatores comuns e incomuns de 6, 8 e 12 com seu maior expoente, então:

lcm (6,8,12) = 2³ ⋅3 = 8 × 3 = 24

Como temos o mínimo múltiplo comum, ele deve ser multiplicado por cada um dos termos da equação:

4 (x + 5) -3 (2x + 3) = 2 (1-5x)

Fazemos uso da propriedade distributiva:

4x + 20 - 6x -9 = 2 - 10x

Todos os termos que contêm o "x" desconhecido são agrupados no lado esquerdo da igualdade, deixando os termos independentes ou numéricos no lado direito:

4x - 6x + 10 x = 2 +9 - 20

8x = -9

x = - 9/8

Equações literais

São equações lineares com uma incógnita, mas são acompanhadas por coeficientes literais (letras). Essas letras são tratadas da mesma forma que os números. Um exemplo de equação literal de primeiro grau é:

-3ax + 2a = 5x - b

Esta equação é resolvida da mesma maneira como se os termos e coeficientes independentes fossem numéricos:

-3ax - 5x = - b - 2a

Fatorando o desconhecido "x":

x (-3a - 5) = - b - 2a

x = (- b - 2a) / (-3a - 5) → x = (2a + b) / (3a + 5)

Sistemas de equações de primeiro grau

Os sistemas de equações consistem em um conjunto de equações com duas ou mais incógnitas. A solução do sistema consiste em valores que satisfaçam as equações simultaneamente e para determiná-la de forma inequívoca, deve haver uma equação para cada incógnita.

A forma geral de um sistema de m equações lineares com n incógnitas é:

para₁₁x₁ + a₁₂x₂+ ... para_1nx_n = b₁
para₂₁x₁ + a₂₂x₂+ ... para_2nx_n = b₂
…
para_m1x₁ + a_m2x₂+ ... para_mnx_n = b_m

Se o sistema tem uma solução, diz-se que é compatível determinado, quando há um conjunto infinito de valores que o satisfazem, é indeterminado compatívele, finalmente, se não tiver solução, então é incompatível.

Vários métodos são usados na resolução de sistemas de equações lineares: redução, substituição, equalização, métodos gráficos, eliminação de Gauss-Jordan e o uso de determinantes estão entre os mais usados. Mas existem outros algoritmos para chegar à solução, mais convenientes para sistemas com muitas equações e incógnitas.

Um exemplo de sistema de equações lineares com duas incógnitas é:

8x - 5 = 7a - 9
6x = 3y + 6

A solução deste sistema é apresentada posteriormente na seção de exercícios resolvidos.

Equações lineares com valor absoluto

O valor absoluto de um número real é a distância entre sua localização na reta numérica e 0 na reta numérica. Por se tratar de uma distância, seu valor é sempre positivo.

O valor absoluto de um número é denotado pelas barras do módulo: │x│. O valor absoluto de um número positivo ou negativo é sempre positivo, por exemplo:

│+8│ = 8

│-3│ = 3

Em uma equação de valor absoluto, a incógnita está entre as barras de módulo. Vamos considerar a seguinte equação simples:

│x│ = 10

Existem duas possibilidades, a primeira é que x é um número positivo, caso em que temos:

x = 10

E a outra possibilidade é que x seja um número negativo, neste caso:

x = -10

Estas são as soluções desta equação. Agora vamos ver um exemplo diferente:

│x + 6│ = 11

O valor dentro das barras pode ser positivo, então:

x + 6 = 11

x = 11 -6 = 5

Ou pode ser negativo. Em tal caso:

- (x + 6) = 11

-x - 6 = 11 ⇒ -x = 11 + 6 = 17

E o valor do desconhecido é:

x = -17

Esta equação de valor absoluto, portanto, tem duas soluções: x₁ = 5 e x₂ = -17. Podemos verificar se ambas as soluções levam a uma igualdade na equação original:

│5+6│ = 11

│11│ = 11

│-17+6│ = 11

│-11│ = 11

Exercícios resolvidos simples

- Exercício 1

Resolva o seguinte sistema de equações lineares com duas incógnitas:

8x - 5 = 7y -9
6x = 3y + 6

Solução

Conforme proposto, este sistema é ideal para a utilização do método de substituição, uma vez que na segunda equação a incógnita x está quase pronto para liberação:

x = (3y + 6) / 6

E pode ser substituído imediatamente na primeira equação, que então se torna uma equação de primeiro grau com "y" desconhecido:

8 [(3y + 6) / 6] - 5 = 7y - 9

O denominador pode ser suprimido multiplicando cada termo por 6:

6 8⋅ [(3y + 6) / 6] - 6,5 = 6,7y– 6. 9

8⋅ (3y + 6) - 30 = 42y - 54

Aplicando a propriedade distributiva no primeiro termo ao direito da igualdade:

24a + 48 -30 = 42a - 54 ⇒ 24a + 18 = 42a - 54

A equação pode ser simplificada, uma vez que todos os coeficientes são múltiplos de 6:

4y + 3 = 7y - 9

-3y = -12

y = 4

Com este resultado vamos ao apuramento de x:

x = (3y +6) / 6 → x = (12 + 6) / 6 = 3

- Exercício 2

Resolva a seguinte equação:

Solução

Os produtos aparecem nesta equação e, seguindo as instruções fornecidas no início, devem ser desenvolvidos primeiro:

3x - 10x +14 = 5x + 36x + 12

Então, todos os termos que contêm as incógnitas são levados para o lado esquerdo da igualdade, e para o lado direito serão os termos independentes:

3x - 10x - 5x - 36x = 12 - 14

-48x = -2

x = 1/24

- Exercício 3

Adicionar os três ângulos internos de um triângulo resulta em 180º. O mais alto excede o menor em 35º, e este por sua vez excede a diferença entre o maior e o médio em 20º. Quais são os ângulos?

Solução

Chamaremos "x" para o ângulo maior, "y" para o do meio e "z" para o menor. Quando o enunciado afirma que a soma deles é 180º, pode-se escrever:

x + y + z = 180

Então sabemos que o maior supera o menor em 35º, podemos escrever assim:

x = z + 35

Por fim, o menor supera em 20º a diferença entre o maior e o médio:

z = x - y + 20

Temos um sistema de 3 equações e 3 incógnitas:

x + y + z = 180

x = z + 35

z = x - y + 20

Resolvendo para z a partir da primeira equação, temos:

z = 180 - x - y

Combinando com o terceiro:

180 - x - y = x - y + 20

Passando as incógnitas para o lado esquerdo como sempre:

-x - y - x + y = 20 - 180

O "y" é cancelado e permanece:

-2x = - 160

x = 80º

A partir da segunda equação, encontramos o valor de z:

z = x - 35 = 80 - 35 = 45º

E o valor de y é encontrado a partir do primeiro ou terceiro:

y = 180 - x - z = 180 - 80 - 45 = 55º

Referências

Baldor. 1977. Elementary Algebra. Edições culturais venezuelanas.
Monterey Institute. Equações, desigualdades e valor absoluto. Recuperado de: montereyinstitute.org.
Professor online. Classificação de equações lineares ou de primeiro grau. Recuperado de: profesorenlinea.cl.
Hoffman, J. Selection of Mathematics Topics. Volume 2.
Jiménez, R. 2008. Algebra. Prentice Hall.
Zill, D. 1984. Algebra and Trigonometry. McGraw Hill.